Elimination Grid notes & advanced hints
The Elimination Grid depicts an effective method for solving a Sudoku puzzle: Lightly pencil in all numbers that are possible for each unsolved cell. This, of course, is a simple matter of eliminating from each unsolved cell any number which is already in place in the same row, column, or 3x3 square, pencilling into each cell only those numbers that remain.Return to the main Sudoku Analyzer page.
For some unsolved cells, only one possibility will remain after such an elimination process. You may confidently assign the lone possibility to that cell, which makes it a solved cell, and you are one step closer to solving the whole Sudoku puzzle. (When you do this on paper, remember to now erase the number from all other unsolved cells in the same row, column and 3x3.)
The next step is to look for instances where there is only one cell in a given row, column, or 3x3 square that can contain a particular value. Again, that cell can now be considered solved, and you may eliminate the number from all other cells in the same row, column and 3x3.
If no cells can be solved in the above ways, more advanced techniques may be employed.
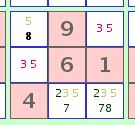
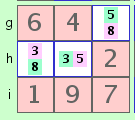
For example, 2 cells within the same 3x3 may both contain only the 2 possibilities '3' and '5' (a 'Naked Pair'). You may not yet be able to determine which cell contains the '3' and which contains the '5'. But since those 2 cells must 'use up' those 2 numbers, no other cell in the same 3x3 may contain either a '3' or a '5'. All such possibilities for a '3' or '5' may be eliminated, which may help solve one of those other cells. In the illustration, eliminating the '5' from the upper left cell leaves only one possible number for that cell. In the same way, 3 cells in the same row, column or 3x3 may 'monopolize' 3 numbers ('Naked Trips'), and 4 cells may monopolize 4 numbers ('Naked Quads').
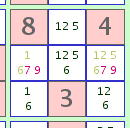
For example, 2 cells within a 3x3 may contain the 2 possibilities '7' and '9'. If those two digits are not possible within other cells in the same 3x3, they must be found in those two cells (a 'Hidden Pair'), and all other digits for those two cells may be eliminated. In the illustration, this step results in no solved cell, but may well lead to a solution elsewhere.
This is the exact inverse of 'Note 1' above. In the illustrated example, we could also have found that the 4 digits '1', '2', '5', and '6' were 'Naked Quads', monopolized by the other 4 unsolved cells, thereby eliminating these 4 digits from the 2 cells, leaving only the possibilities '7' and '9'. It's mostly just a matter of which pattern is easier to spot.
For example, the number '4' may be possible in 2 or 3 unsolved cells in one 3-cell row. Then check the other 6 cells in the same 3x3 square and the other 6 cells in the same full row, whether any of them also contain a possible '4'. If the answer is 'Yes' for the full row and 'No' for the 3x3, you may eliminate the number '4' from those other 6 cells in the same full row.
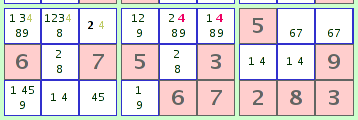
Here's why: The 3x3 square must get its '4' from one of those 3 cells within the 3x3 row, so the other 6 cells within the full row may not contain a '4'. (If they did, there would be no place for a '4' in the 3x3, and the 3x3 would become unsolvable.) In the illustration, eliminating the '4' from other cells in the full row results in the third cell from the left being solved.
In the same way, if the answer were 'Yes' for the 3x3 and 'No' for the row, you could eliminate '4' from the other 6 cells within the 3x3. This logic also applies to the 3-cell intersection of 3x3 squares with columns.
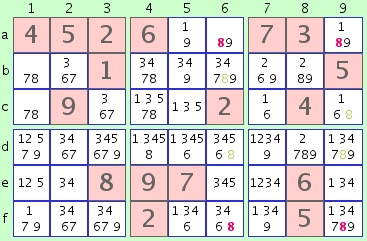
For example, the number '8' may be possible in the 4 unsolved cells 'a6', 'a9', 'f6', and 'f9'. If there are no other possibilities for an '8' in other unsolved cells in rows 'a' and 'f', these two rows must each get its '8' from one of the X-wing cells. Since those two '8's must not be in the same column nor in the same row, they must therefore be in opposite corners ('a6/f9' or 'a9/f6'). It then follows that each of the two columns '6' and '9' must also get its '8' from those same opposite corners of the X-wing, and that therefore no other cells in columns '6' or '9' may contain an '8'. In the illustration, this means we can eliminate the '8' from cells 'b6', 'd6', 'c9', and 'd9'.
In the same way, if there had been no other possibilities for an '8' in columns '6' and '9', we could have eliminated any '8' in other cells in rows 'a' and 'f'.
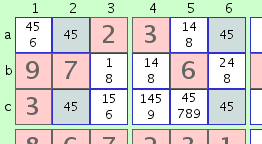 The deadly pattern. The 4 cells a2-a6-c2-c6 in the figure illustrate an example of an unsolvable 'deadly pattern'. We may be able to solve all the other cells of this Sudoku, but the deadly pattern will prevent us from solving these 4 cells. This Sudoku will end up having one solution with a '4' in cells 'a2' and 'c6' and a '5' in 'a6' and 'c2', and another solution in the opposite order. Since these 4 cells occupy exactly two rows, two columns and two 3x3 boxes, each of the columns, rows and 3x3s will allow either order, and therefore the Sudoku will have two solutions, which is to say, it will be an invalid multiple-solution Sudoku puzzle. Note that if the 4 cells were to occupy 4 different 3x3 boxes, the 3x3s would not allow both orders, and the deadly pattern would not exist.
The deadly pattern. The 4 cells a2-a6-c2-c6 in the figure illustrate an example of an unsolvable 'deadly pattern'. We may be able to solve all the other cells of this Sudoku, but the deadly pattern will prevent us from solving these 4 cells. This Sudoku will end up having one solution with a '4' in cells 'a2' and 'c6' and a '5' in 'a6' and 'c2', and another solution in the opposite order. Since these 4 cells occupy exactly two rows, two columns and two 3x3 boxes, each of the columns, rows and 3x3s will allow either order, and therefore the Sudoku will have two solutions, which is to say, it will be an invalid multiple-solution Sudoku puzzle. Note that if the 4 cells were to occupy 4 different 3x3 boxes, the 3x3s would not allow both orders, and the deadly pattern would not exist.The certainty that we have a valid single-solution Sudoku which may not contain such a deadly pattern is the basis for the following 3 cases:
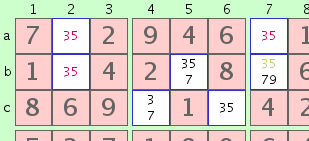 Unique Rectangle - Case A
Unique Rectangle - Case AIt may happen that the same 2 possible digits exist in the 4 cells of a rectangle, but that in exactly one of those cells there also exists the possibility of one or more other numbers. Since these other possibilities are the only way to avoid the deadly pattern, we know they must exist, and that allows us to eliminate from that cell the two digits of the deadly pattern. In the example rectangle a2-a7-b2-b7, we know that cell 'b7' must contain a '7' or '9', so we can eliminate the deadly pattern numbers '3' and '5' from that cell.
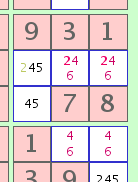 Unique Rectangle - Case B
Unique Rectangle - Case BAnother 'Unique Rectangle' case is one in which 2 of the 4 cells contain the same single alternate number to the two deadly pattern numbers. If these two cells lie in the same column or the same row, we can employ this strategy. In order to avoid the deadly pattern, the alternate digit must exist in one of those 2 cells of the rectangle. This digit can therefore be eliminated from any cell outside the rectangle but in the same row, column, or 3x3 as both of those 2 cells.
In the illustration, to avoid the deadly pattern, we can be confident that one of the two top cells of the rectangle must contain a '2'. This allows us to eliminate the '2' from a cell outside of the rectangle but in the same row, leaving only a '4' or '5' possible in that cell.
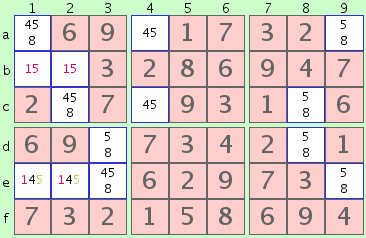 Unique Rectangle - Case C
Unique Rectangle - Case CA third 'Unique Rectangle' case is one in which 2 of the 4 cells contain the possibility of one or more alternative numbers, and, as above, these two cells lie in the same column or the same row. Furthermore, if one of the two deadly pattern numbers must exist within one of those two cells, we can safely say that 1) one of the two cells must contain the necessary deadly pattern number, and 2) the other must contain an alternate number. We may therefore eliminate the unnecessary deadly pattern number from both of those 2 cells.
In rectangle b1-b2-e1-e2 in the illustration, we can see that the deadly pattern number '1' must exist in either cell 'e1' or 'e2' since it is not possible in any other cell within the same row or 3x3. But to avoid the deadly pattern, the non-deadly digit '4' must also exist in one of those same 2 cells. This allows us to eliminate the other deadly pattern number '5' from both 'e1' and 'e2'.
An even more advanced technique, called 'Mutually exclusive pairs', consists in building chains of mutually exclusive pairs of candidates, looking for conflicts, and thereby eliminating invalid numbers. This strategy is explained in greater detail in its own help page
Clear as mud? Perhaps you could wait until you actually encounter one of these situations, then re-read these explanations, referring to the Elimination Grid at the same time.
That is to say, I know of no other nifty Sudoku technique that will solve a tough Sudoku where my Sudoku Analyzer fails. If you disagree, I'd be eager to hear from you. Also welcome are more general inquiries and suggestions. You may use this website's Contact page for various ways to reach me.